This week I published the preprint of a manuscript that started as a blog post, but quickly out-grew this medium: Understanding the Lomb-Scargle Periodogram.

Figure 24 from Understanding the Lomb-Scargle Periodogram. The figure shows the true period vs the periodogram peak for a simulated dataset with an observing cadence typical of ground-based optical astronomy. The simulation reveals common patterns of failure of the Lomb-Scargle method that are not often discussed explicitly, but are straightforward to explain based on the intuition developed in the paper; see Section 7.2 for a detailed discussion.

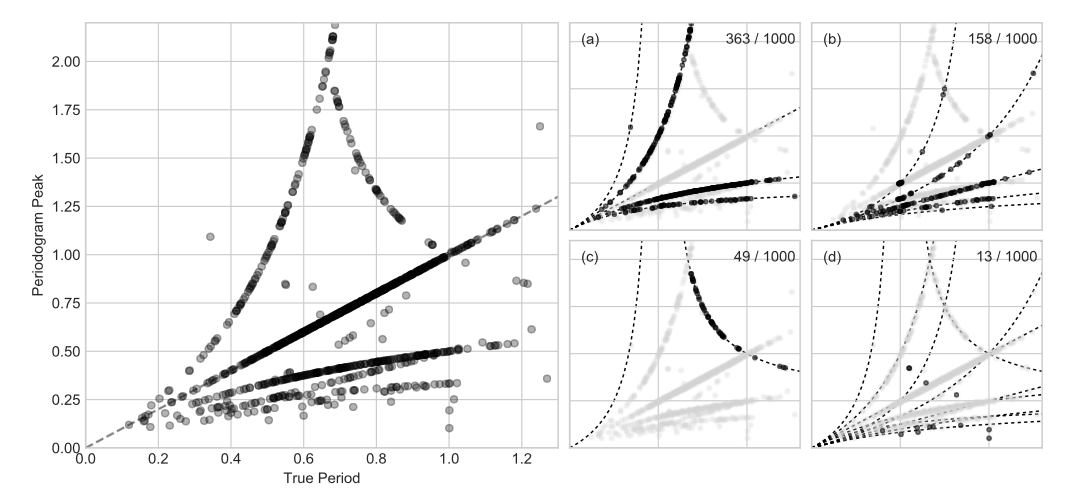Over the last couple years I've written a number of Python implementations of the Lomb-Scargle periodogram (I'd recommend AstroPy's LombScargle in most cases today), and also wrote a marginally popular blog post and somewhat pedagogical paper on the subject. This all has led to a steady trickle of emails from students and researchers asking for advice on applying and interpreting the Lomb-Scargle algorithm, particularly for astronomical data. I noticed that these queries tended to repeat many of the same questions and express some similar misconceptions, and this paper is my attempt to address those once and for all — in a "mere" 55 pages (which includes 26 figures and 4 full pages of references, so it's not all that bad).

While the paper's main goal is to help readers develop an intuition for what the periodogram actually measures and how this affects practical considerations of its use, I also took the opportunity to directly address some of the mythology that's been built-up around the algorithm. I'll let those who are interested read the full paper (you can also peruse the code and re-generate the figures via Jupyter Notebooks on GitHub), but I want to highlight here my somewhat opinionated post-script outlining some of these myths, and considering whether we should be using the Lomb-Scargle method at all.

The following is copied verbatim from the final section of the manuscript:

Postscript: Why Lomb-Scargle?

After considering all of these practical aspects of the periodogram, I think it is worth stepping back to revisit the question of why astronomers tend to gravitate toward the Lomb-Scargle approach rather than the (in many ways simpler) classical periodogram.

As discussed in Section 5, the Lomb-Scargle approach has two distinct benefits over the classical periodogram: the noise distribution at each individual frequency is chi-square distributed under the null hypothesis, and the result is equivalent to a periodogram derived from a least squares analysis. But somehow along the way, a mythology seems to have developed surrounding the efficiency and efficacy of the Lomb-Scargle approach. In particular, it’s common to see statements or implications along the lines of the following:

• Myth: The Lomb-Scargle periodogram can be computed more efficiently than the classical periodogram. Reality: computationally, the two are quite similar, and in fact the fastest Lomb-Scargle algorithm currently available is based on the classical periodogram computed via the the NFFT algorithm (see Section 7.6).
• Myth: The Lomb-Scargle periodogram is faster than a direct least squares periodogram because it avoids explicitly solving for model coefficients. Reality: model coefficients can be determined with little extra computation (see the discussion in Ivezic et al. 2014).
• Myth: The Lomb-Scargle periodogram allows analytic computation of statistics for periodogram peaks. Reality: while this is true at individual frequencies, it is not true for the more relevant question of maximum peak heights across multiple frequencies, which must be either approximated or computed by bootstrap resampling (see Section 7.4)
• Myth: The Lomb-Scargle periodogram corrects for aliasing due to sampling and leads to independent noise at each frequency. Reality: for structured window functions common to most astronomical applications, the Lomb-Scargle periodogram has the same window-driven issues as the classical periodogram, including spurious peaks due to partial aliasing, and highly correlated periodogram errors (see Section 7.2).
• Myth: Bayesian analysis shows that Lomb-Scargle is the optimal statistic for detecting periodic signals in data. Reality: Bayesian analysis shows that Lomb-Scargle is the optimal statistic for fitting a sinusoid to data, which is not the same as saying it is optimal for finding the frequency of a generic, potentially non-sinusoidal signal (see Section 6.5).

With these misconceptions corrected, what is the practical advantage of Lomb-Scargle over a classical periodogram? What would we lose if we instead used the simple classical Fourier periodogram, estimating uncertainty, significance, and false alarm probability by resampling and simulation, as we must for Lomb-Scargle itself?

The advantage of analytic statistics for Lomb-Scargle evaporates in light of the need to account for multiple frequencies, so the only advantage left is the correspondence to least squares and Bayesian models, and in particular the ability to generalize to more complicated models where appropriate—but in this case you’re not really using Lomb-Scargle at all, but rather a generative Bayesian model for your data based on some strong prior information about the form of your signal. The equivalence of Lomb-Scargle to a Bayesian sinusoidal model is perhaps an interesting bit of trivia, but not itself a reason to use that model if your data is not known a priori to be sinusoidal—it could even be construed as an argument against Lomb-Scargle in the general case where the assumption of a sinusoid is not well-founded.

Conversely, if you replace your Lomb-Scargle approach with a classical periodogram, what you gain is the ability to reason quantitatively about the effects of the survey window function on the resulting periodogram (cf. Section 7.3). While the deconvolution problem is ill-posed, there is no reason to assume this is a fatal defect: ill-posed linear models are solved routinely in other areas of computational research, particularly by using sparsity priors or various forms of regularization. In any case, I would contend that there is ample room for practitioners to question the prevailing folk wisdom of the advantage of Lomb-Scargle over approaches based directly on the Fourier transform and classical periodogram.

I think these are questions worth wrestling with.

Although a number of colleagues gave me immensely helpful feedback on early drafts, the paper has not yet gone through any formal peer review process. To this end I plan to submit the manuscript to a relevant ApJ special issue that is coming together later this year. In the meantime, if you have any comments or critiques on the draft, I'd greatly value your feedback. Feel free to comment here on the blog, or better, to open a GitHub Issue.

Thanks for reading!