LombScargle

class lombscargle.LombScargle(t, y, dy=None, fit_bias=True, center_data=True)

Bases: object

Compute the Lomb-Scargle Periodogram

Parameters:

t : array_like or Quantity

sequence of observation times

y : array_like or Quantity

sequence of observations associated with times t

dy : float, array_like or Quantity (optional)

error or sequence of observational errors associated with times t

fit_bias : bool (optional, default=True)

if True, include a constant offet as part of the model at each frequency. This can lead to more accurate results, especially in then case of incomplete phase coverage.

center_data : bool (optional, default=True)

if True, pre-center the data by subtracting the weighted mean of the input data. This is especially important if fit_bias = False

Examples

Generate noisy periodic data:

>>> rand = np.random.RandomState(42)
>>> t = 100 * rand.rand(100)
>>> y = np.sin(2 * np.pi * t) + rand.randn(100)

Compute the Lomb-Scargle periodogram on an automatically-determined frequency grid & find the frequency of max power:

>>> frequency, power = LombScargle(t, y).autopower()
>>> frequency[np.argmax(power)]
1.0016662310392956

Compute the Lomb-Scargle periodogram at a user-specified frequency grid:

>>> freq = np.arange(0.8, 1.3, 0.1)
>>> LombScargle(t, y).power(freq)
array([ 0.0204304 ,  0.01393845,  0.35552682,  0.01358029,  0.03083737])

If the inputs are astropy Quantities with units, the units will be validated and the outputs will also be Quantities with appropriate units:

>>> from astropy import units as u
>>> t = t * u.s
>>> y = y * u.mag
>>> frequency, power = LombScargle(t, y).autopower()
>>> frequency.unit
Unit("1 / s")
>>> power.unit
Unit(dimensionless)

Note here that the Lomb-Scargle power is always a unitless quantity, because it is related to the 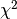of the best-fit periodic model at each frequency.

Methods Summary

autofrequency(t[, heuristic])	Determine a suitable frequency grid for data
autopower([frequency_heuristic, method, ...])	Compute the Lomb-Scargle power at the given frequencies
model(t, frequency)	Compute the Lomb-Scargle model at the given frequency
power(frequency[, normalization, method, ...])	Compute the Lomb-Scargle power at the given frequencies

Methods Documentation

classmethod autofrequency(t, heuristic='baseline', **kwds)

Determine a suitable frequency grid for data

Parameters:

t : array_like or Quantity

The sampling times of the data

heuristic : string

The type of heuristic to use. Currently only ‘baseline’ is supported

**kwds :

additional keyword arguments will be passed to the frequency heuristic.

Returns:

frequency : ndarray or Quantity

The heuristically-determined optimal frequency bin

autopower(frequency_heuristic='baseline', method='auto', method_kwds=None, normalization='normalized', **kwargs)

Compute the Lomb-Scargle power at the given frequencies

Parameters:

frequency_heuristic : string (optional, default=’baseline’)

the frequency heuristic to use. By default, it is assumed that the observation baseline will drive the peak width.

method : string (optional)

specify the lomb scargle implementation to use. Options are:

• ‘auto’: choose the best method based on the input
• ‘fast’: use the O[N log N] fast method. Note that this requires evenly-spaced frequencies: by default this will be checked unless assume_regular_frequency is set to True.
• slow: use the O[N^2] pure-python implementation
• chi2: use the O[N^2] chi2/linear-fitting implementation
• fastchi2: use the O[N log N] chi2 implementation. Note that this requires evenly-spaced frequencies: by default this will be checked unless assume_regular_frequency is set to True.
• scipy: use scipy.signal.lombscargle, which is an O[N^2] implementation written in C. Note that this does not support heteroskedastic errors.

method_kwds : dict (optional)

additional keywords to pass to the lomb-scargle method

normalization : string (optional, default=’normalized’)

Normalization to use for the periodogram. Options are ‘normalized’ or ‘unnormalized’.

**kwargs :

additional keyword arguments will be passed to the frequency heuristic.

Returns:

frequency, power : ndarrays

The frequency and Lomb-Scargle power

model(t, frequency)

Compute the Lomb-Scargle model at the given frequency

Parameters:

t : array_like, length n_samples

times at which to compute the model

frequency : float

the frequency for the model

Returns:

y : np.ndarray, length n_samples

The model fit corresponding to the input times

power(frequency, normalization='normalized', method='auto', assume_regular_frequency=False, method_kwds=None)

Compute the Lomb-Scargle power at the given frequencies

Parameters:

frequency : array_like or Quantity

frequencies (not angular frequencies) at which to evaluate the periodogram. Note that in order to use method=’fast’, frequencies must be regularly-spaced.

method : string (optional)

specify the lomb scargle implementation to use. Options are:

• ‘auto’: choose the best method based on the input
• ‘fast’: use the O[N log N] fast method. Note that this requires evenly-spaced frequencies: by default this will be checked unless assume_regular_frequency is set to True.
• slow: use the O[N^2] pure-python implementation
• chi2: use the O[N^2] chi2/linear-fitting implementation
• fastchi2: use the O[N log N] chi2 implementation. Note that this requires evenly-spaced frequencies: by default this will be checked unless assume_regular_frequency is set to True.
• scipy: use scipy.signal.lombscargle, which is an O[N^2] implementation written in C. Note that this does not support heteroskedastic errors.

assume_regular_frequency : bool (optional)

if True, assume that the input frequency is of the form freq = f0 + df * np.arange(N). Only referenced if method is ‘auto’ or ‘fast’.

normalization : string (optional, default=’normalized’)

Normalization to use for the periodogram. Options are ‘normalized’ or ‘unnormalized’.

fit_bias : bool (optional, default=True)

if True, include a constant offet as part of the model at each frequency. This can lead to more accurate results, especially in the case of incomplete phase coverage.

center_data : bool (optional, default=True)

if True, pre-center the data by subtracting the weighted mean of the input data. This is especially important if fit_bias = False

method_kwds : dict (optional)

additional keywords to pass to the lomb-scargle method

Returns:

power : ndarray

The Lomb-Scargle power at the specified frequency